Recently I’ve been retaking some classes that I had taken a few years ago, now with much more experience and a better mindset to learn. Specifically, I’m retaking Stanford’s Algorithms: Design and Analysis class on Coursera.
In doing so, I’ve gained a significant amount of appreciation for the elegant techniques and methods that algorithm developers have found. Most recently, I learned about Kosaraju’s algorithm for finding strongly connected components (SCCs) in a directed graph, and I thought it was ridiculously elegant and clean.
You’re never going to use Kosaraju’s Algorithm in real life. In fact, there’s a faster solution to this problem using Tarjan’s Algorithm. That’s not the point of studying algorithms. I’m still making my way through Stanford’s Algorithms course, but I’m not just learning about algorithms and how to analyze them. What I’m really learning is how to apply these problem-solving principles that are the foundation of all clever algorithm design.
Strongly Connected Components ¶
In an undirected graph, it’s clear to see what a “connected” component is. If two nodes have a path between them, they are connected, and the connected components are the chunks of nodes that aren’t isolated.
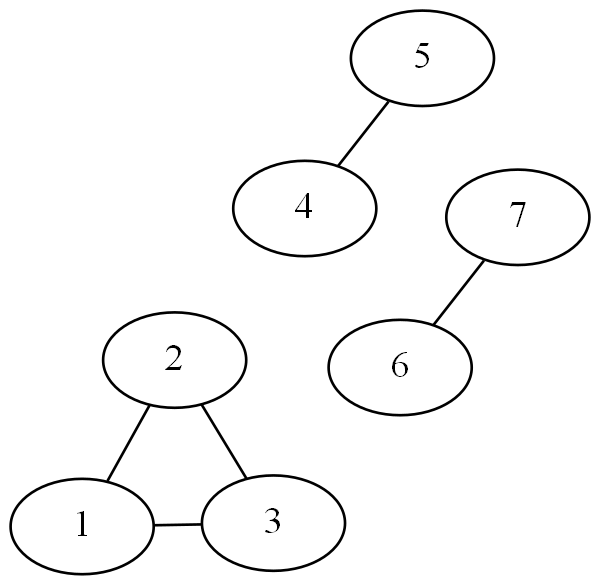
Three Connected Components
Above, the nodes 1, 2, and 3 are connected as one group, 4 and 5, as well as 6 and 7, are each a group as well. It is super clear what the different components in this graph are, and determining connected components in an undirected graph is a piece of cake.
So what happens when we start talking about directed graphs?
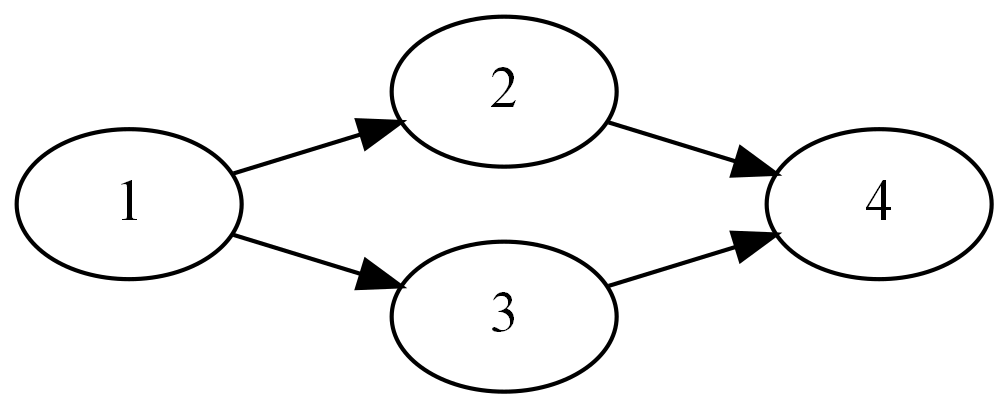
How many "connected components" exist in this graph?
Well, just looking at it like we did earlier, there is only one group of connected nodes. So there’s only one connected component, right?
Trick question. To answer that question, we need to define connected components for directed graphs.
Definition ¶
A more theoretical definition of SCCs would talk about equivalence relations and subgraphs, but we don’t care about that. A Strongly Connected Component is the smallest section of a graph in which you can reach, from one vertex, any other vertex that is also inside that section. In slightly more theoretical terms, an SCC is a strongly connected subgraph of some larger graph G.
So that graph above has four SCCs. Every single node is its own SCC. If I go to node 2, I can never go to any other node, and then back to node 2. I’m going to leave it as an exercise to the reader to prove, or at least think about, the idea that for any given directed acyclic graph (DAG) with n nodes, there are exactly n SCCs.
Why? ¶
Okay, cool, we can define and reason about SCCs in graphs. So what, why do we care?
I mean honestly, it’s just cool. It’s a nice way to reason about and visualize complicated graphs, and you can use SCCs to analyze and think about larger graphs like social media networks or even the internet. SCCs can also be used to simplify the 2-SAT problem, but that’s beyond our scope.
Almost 30% of the internet is strongly connected
It’s just cool, we can learn and understand a lot about large networks. Pinpoint weak points, make pretty diagrams, whatever you desire. But what’s even cooler is some of the ingenuity behind the algorithms that one might use to find SCCs.
Finding normal connected components ¶
Before we dive into Kosaraju’s Algorithm, let’s discuss how we’d calculate the connected components in an undirected graph. If we do a DFS (or BFS), on a given node, we’ll find all the connected nodes. If we iterate over every single node and DFS, whenever we iterate over a node that hasn’t been seen, it’s a connected component. The (python-esque) pseudocode might look something like:
def dfs_loop(G):
n = 0
for node in G:
if not node.visited:
n++
dfs(G, node)
def dfs(G, v):
v.visited = True
for edge:(v, w) in G:
if not w.visited:
dfs(G, w)
and now n will count the number of components in an undirected graph. What if we tried this on a directed graph?
Counting SCCs ¶
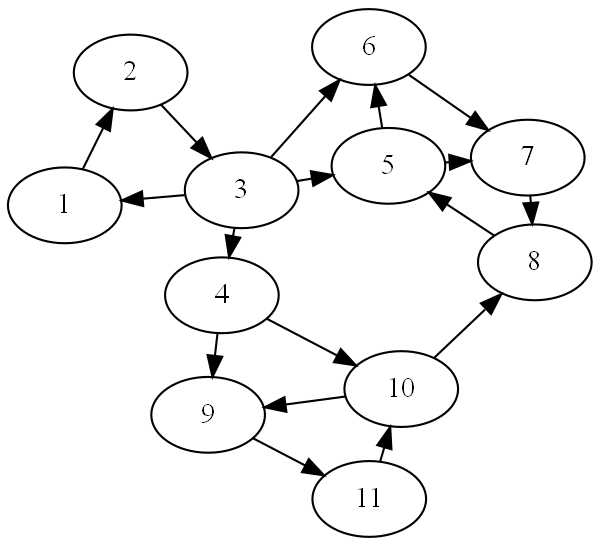
An example
There are 4 strongly connected components in this graph G: {1, 2, 3}, {4}, {5, 6, 7, 8}, {9, 10, 11}. Let’s try that same method on this example graph. Say we start at node 10, we’ll hit 9 and 10, and only those three nodes. Okay, that was easy. What if we start at node 3? We’ll hit 1, 2, 4, 5…
So our method works, sometimes. What do we do?
Kosaraju’s Algorithm ¶
Let’s apply some intuition. If we “compressed” this graph, converting each set of SCCs into one supernode, we’d get a simple set of 4 nodes. In fact, we get that same graph that we saw earlier. This graph is a DAG, it ends. If we start in one of the “sink” SCCs, we will only find the things in that SCC. We can keep working our way backward, and every time we call DFS, we will only see the nodes in that SCC.
Kosaraju’s Algorithm applies this idea to find all the SCCs in a given graph in linear time. We do one DFS pass trying to find the correct order of nodes, and then we do another pass going in that order.
How do we find that correct order? Ideally, we want to be starting in one of the sink SCCs. If we do a normal post-order DFS, we can be certain that the last node is not going to be inside of a sink SCC. The first node may be inside a sink SCC, but we can’t be sure. However, if we do a post-order DFS on the reversed graph, we know that the last node will be inside of a sink SCC. This reversed order is the correct order. I urge you to validate this yourself, as it might not be instantly clear, but you’ll find that this is indeed true.
Using this knowledge, we just need to do two passes of DFS. One on the reversed graph, and one in the newfound order.
At the suggestion of aneksteind, if you’re interested in an actual implementation of Kosaraju’s Algorithm, take a look at their gist. Or, just in some psuedocode:
s = None
order = []
def dfs_loop(G):
for node in G:
if not node.explored:
s = node
dfs(G, node)
def dfs(G, v):
v.explored = True
v.leader = s
for edge:(v, w):
if not w.explored:
dfs(G, w)
order = [v] + order
def kosaraju(G):
dfs_loop(G_reversed)
dfs_loop(G) in order
Ridiculously simple, ridiculously clever. Each node’s “leader” is the first node that we encountered within it’s SCC. We can now group by the leader and find each SCC.
We started with some fundamental ideas, worked with DAGs, which we’re a little more comfortable with, and then reduced the problem until the answer becomes more and more intuitive. I hope you learned something new and gained some insight into problem-solving because I certainly did.